 Tony Jebara
- - Research
Tony Jebara
- - Research
 Tony Jebara
- - Research
Tony Jebara
- - Research
|
|
 home
home research
research papers
papers courses
courses resumé
resumé code
code press
press  hobbies
hobbies trips
trips links
links |
|||||||||
|
|
|||||||||
|
Tony directs the Columbia Machine Learning
Laboratory. Our research area is machine learning, a field which
develops novel algorithms that use data to model complex real-world
phenomena and to make accurate predictions about them. Our work spans
both the applied and the fundamental aspects of the field. We have
made contributions by migrating generalized matching, graph-theoretic
methods and combinatorial methods into the field of machine
learning. We have also introduced unifying frameworks that combine two
separate methodologies in the field: discriminative approaches and
generative approaches. The machine learning applications we have
worked on have had real-world impact achieving state of the art
results in vision, face recognition and spatio-temporal tracking,
leading to a successful startup which applies machine learning
to spatio-temporal data. Our papers are available online here.
For a Russian translation of this web-page click here. Learning with Matchings and Perfect GraphsLearning with Generalized MatchingsWe are interested in the application of generalized matching and other graph-theoretic / combinatorial methods to machine learning problems. Matching is an important tool in many fields and settings. One famous example of generalized matching is Google's AdWords system which approximately matches advertisers to search terms (AdWords generates a significant portion of Google's revenue). Until recently, matching has had limited impact in machine learning. In the past 5 years, we have introduced and explored the connections between machine learning problems and generalized matching. In 1965, Jack Edmonds began pioneering work into the combinatorics of matching and its many extensions including b-matching. This work received the following citation during Edmonds' receipt of the 1985 John von Neumann Theory Prize, Jack Edmonds has been one of the creators of the field of combinatorial optimization and polyhedral combinatorics. His 1965 paper "Paths, Trees, and Flowers" was one of the first papers to suggest the possibility of establishing a mathematical theory of efficient combinatorial algorithms.Matchings and generalized matchings are a family of graphs (such as trees) that enjoy fascinating combinatorics and fast algorithms. Matching goes by many names and variations including permutation (or permutation-invariance), assignment, auction, alignment, correspondence, bipartite matching, unipartite matching, generalized matching and b-matching. The group of matchings is called the symmetric group in algebra. We introduced the use of matching in machine learning problems and showed how it improves the state of the art in machine learning problems like classification, clustering, semisupervised learning, collaborative filtering, tracking, and visualization. We have also shown how matching leads to theoretical and algorithmic breakthroughs in MAP estimation, Bayesian networks and graphical modeling which are important topics in machine learning. We initially explored matching from a computer vision perspective where it was already a popular tool. For instance, to compare two images for recognition purposes, it is natural to first match pixels or patches in the images by solving a bipartite matching problem. We first explored matching for this type of image alignment and interleaved it into unsupervised and supervised learning problems. For instance, we explored matching within unsupervised Gaussian modeling and principal components analysis settings (ICCV 03, AISTAT 03, COLT 04). We also explored matching in classification frameworks by building kernels that were invariant to correspondence (ICML 03) and classifiers that were invariant to permutation (ICML 06b). These methods significantly outperformed other approaches particularly on image datasets when images were represented as vector sets or bags of pixels (ICCV 03). The paper A Kernel between Sets of Vectors (ICML 03) won an award at the International Conference on Machine Learning in 2003 out of a total of 370 submitted papers. Given the empirical success of matching in image problems, we considered its application to other machine learning problems. One key insight was that matching acts as a general tool for turning data into graphs. Once data is in the form of a graph, a variety of machine learning problems can be directly handled by algorithms from the graph theory community. We began pioneering the use of b-matching, a natural extension to matching in a variety of machine learning problems. We showed how it can lead to state of the art results in visualization or graph embedding (ICML 09, AISTATS 07d), clustering (ECML 06), classification (AISTAT 07b), semisupervised learning (ICML 09b), collaborative filtering (NIPS 08b), and tracking (AISTAT 07a). We were initially motivated by the KDD 2005 Challenge which was a competition organized by the CIA and NSA to cluster anonymized documents by authorship. By using b-matching prior to spectral clustering algorithms, we obtained the best average accuracy in the ER1B competition in competition with 8 funded teams from various other universities. The work was published in a classified journal (Jebara, Shchogolev and Kondor in JICRD 2006) and a related non-classified publication can be found in (ECML 06). A simple way of seeing the usefulness of b-matching is to consider it as a principled competitor to the most popular and simplest machine learning algorithm: k-nearest neighbors. For instance, consider connecting the points in the figure below using 2-nearest-neighbors. Typically, when computing k-nearest-neighbors, many nodes will actually have more than k neighbors since, in addition to choosing k neighbors, each node itself can be selected by other nodes during the greedy procedure. This situation is depicted in Figure (a) below. Here, several two ring datasets are shown and should be clustered into the two obvious components: the inner ring and the outer ring. However, when the smaller ring's radius is similar to the larger ring's radius or when the number of samples on each ring is low, k-nearest-neighbors does not recover the two ring connectivity correctly. This is because nodes in the smaller inner ring get over-selected by nodes in the outer ring and eventually have large neighborhoods. Ultimately, k-nearest neighbor algorithms do not produce regular graphs as an output and the degree for many nodes (especially on the inner ring) is larger than k. This irregularity in k-nearest-neighbors can get exponentially worse in higher dimensional datasets as shown by (Devroye and Wagner, 1979). This limits the stability and generalization power of k-nearest neighbors by the so called kissing number in d-dimensional space. Conversely, b-matching methods guarantee that a truly regular graph (of minimum total edge length) is produced. Figure (b) shows the output of b-matching and therein it is clear that each node has exactly 2 neighbors. Even spectral clustering will not tease apart these two rings at some scales and sampling configurations. 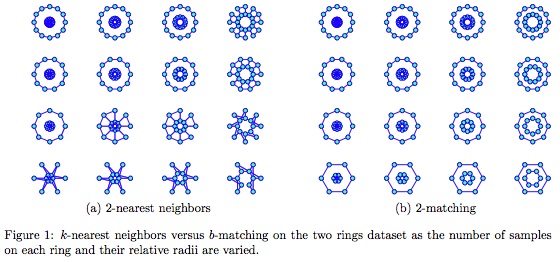
After showing how matching improves spectral clustering in practice (ECML 06), we investigated its use in other machine learning settings. For instance, in (AISTAT 07b), we showed how it can perform more accurate classification than k-nearest neighbors without requiring much more computational effort. In visualization problems where high dimensional datasets are typically turned into k-nearest neighbor graphs prior to low dimensional embedding (AISTATS 07d), we showed how b-matching yields more balanced connectivity and more faithful visualizations (Snowbird 06, ICML 09). The latter paper Structure Preserving Embedding won the best paper award at the International Conference on Machine Learning in 2009 out of a total of 600 submitted papers. In addition, in semisupervised learning and so-called graph transduction methods (ICML 08), we showed how b-matching consistently improves accuracy (ICML 09b). In collaborative filtering problems, we applied a generalization of b-matching where each node need not have constant degree b but rather any customizable distribution over degrees and this yielded more accurate recommendation results (NIPS 08b). Finally, by realizing that matchings form a finite group in algebra known as the symmetric group, we have managed to apply group-theoretic tools such as generalized fast Fourier transforms to solve problems over distributions on matchings (AISTAT 07a). Such distributions over matchings are useful in multi-target tracking since, at each time point, the identity of current targets needs to be matched to previously tracked trajectories. However, since there are n! matchings, these distributions need to be band-limited using Fourier analysis to remain efficient (polynomial). To our knowledge, this was the first application of group theory to matchings in a machine learning and or tracking setting and led to improvement over previous methods. Matching, MAP Estimation and Message PassingOne of the obstacles in applying off the shelf generalized matching solvers to real machine learning problems is computation time. For instance, the fastest solvers from the combinatorial optimization community were too computationally demanding to handle more than a few hundred data points (ECML 06). This led us to build our own algorithms for solving b-matchings by trying a generally fast machine learning approach known as message passing (or belief propagation which is used interchangeably here). This method is extremely popular in machine learning problems and is used to perform approximate inference in graphical models and decomposable probability distributions. In (AISTAT 07b), we realized that b-matching problems could be written as a graphical model, a probability density function that decomposes into a product of cliques in a sparse graph. To find the maximum a posteriori (MAP) estimate of this graphical model, we implemented message passing, a clever and fast way of approximating the b-matching problem by sending messages along the graph. Message passing works for MAP estimation on tree-structured graphical models but only gives approximate answers on graphical models with loops. Since the b-matching graphical model had many loops, all we could hope for was suboptimal convergence some of the time. Amazingly, message passing on this loopy graphical model efficiently produced the correct answer all the time. We published a proof guaranteeing the efficient and exact convergence of message passing for b-matching problems in (AISTAT 07b), and showed one of the few cases where the optimality is provably preserved despite loops in the graphical model. The optimality of message passing for trees (Pearl 1988) and single-loop graphs (Weiss 2000) were previously known however the extension to b-matching represents an important special case. This was significant since defining which graphical models admit exact inference has been an open and exciting research area in the field of machine learning (and other communities such as decoding) for many years. Graphical models corresponding to matching, b-matching and generalized matching extend known guarantees beyond trees and single loop graphs to a wider set of models and problems. Today, the connection between message passing and matching is a promising area of theoretical research with contributions from multiple theory researchers (Bayati, Shah and Sharma 2005, Sanghavi, Malioutov and Willsky 2008, as well as Wainwright and Jordan 2008).Simultaneously, several applied researchers have downloaded our code (available online) and are efficiently solving large scale (bipartite and unipartite) b-matching problems using message passing. Our group uses the code regularly for the various papers described in the previous section. In our original article we proved that the algorithm requires O(n^3) time for solving maximum weight b-matchings on dense graphs with n nodes yet empirically our code seemed to be much more efficient. Recently, (Salez and Shah 2009) proved that, under mild assumptions, message passing methods take O(n^2) on dense graphs. This result indicates that our implementation is one of the fastest around and applies to problems of comparable scale as k-nearest neighbors. Currently, we are working on other theoretical guarantees for b-matching in terms of its generalization performance when applied to independently sampled data. To do so, we are attempting to characterize the stability of b-matching compared to k-nearest neighbors by following the approach of (Devroye and Wagner 1979) which should yield theoretical guarantees on its accuracy in machine learning settings. Matchings, Trees and Perfect GraphsMatchings, b-matchings and generalized matchings are just families of graphs in the space of all possible undirected graphs on n nodes. There are n! possible matchings and even more possible b-matchings. Amazingly, however, maximum weight matchings can be recovered efficiently either by using Edmonds' algorithm or by using matching-structured graphical models which admit exact inference via message passing. Similarly, there are n^(n-2) trees and tree-structured graphical models admit exact inference via message passing.We have worked on tree structured graphical modeling in several settings because of these interesting computational advantages. For instance, in (UAI 04), we developed tree hierarchies of dynamical systems that allow efficient structured mean field inference. These were useful for multivariate time series tracking and other applied temporal data. Another remarkable property of trees is that summation over a distribution over all n^(n-2) trees can be done in cubic time using Kirchoff's and Tutte's theorem. In (NIPS 99) we proposed inference over the distribution of all possible undirected trees over n nodes using Kirchoff's matrix tree theorem. In (UAI 08) we developed inference over the distribution of all possible out directed trees over n nodes using Tutte's matrix tree theorem. These methods are useful in modeling non iid data such as phylogenetic data, disease spread, language arborescence models and so forth. Not only do trees have fascinating combinatorial and computational properties, they lead to important empirical results on real world machine learning problems. Similarly, not only do matchings have fascinating combinatorial and computational properties, they lead to important empirical results on real world machine learning problems. Is there some larger family of graphs which subsumes these two families of graphs? This answer is yes and leads to the most exciting topic in combinatorics: perfect graphs . In (UAI 09) we were the first to identify this contact point between perfect graphs and machine learning and probabilistic inference. Recently, mathematicians and combinatorics experts have had a breakthrough in their field through the work of (Chudnovsky et al. 2006) who proved the decades-old strong perfect graph conjecture and developed algorithms for testing graphs to determine if they are perfect. We have shown that perfect graphs have important implications in the field of machine learning and decoding by using perfect graphs to identify when inference in general graphical models is exact and when it can be solved efficiently via message passing (UAI 09). This is done by converting graphical models (with loops) and the corresponding MAP estimation problem into what we call a nand Markov random field . The topology of this structure is then efficiently diagnosed to see if it forms a perfect graph. If it is indeed perfect, then MAP estimation is guaranteed exact and efficient and message passing will provide the optimal solution. This generalizes known results on trees and the results on generalized matchings to the larger class of perfect graphs. Defining which graphical models admit exact inference has been an open and exciting research area in the field of machine learning (and other communities such as decoding) for many years. Perfect graph theory is now a valuable tool in the field's arsenal. This recent work extends graphical model and Bayesian network inference guarantees that are known about trees and matchings to the more general and more fundamental family of perfect graphs. Discriminative and Generative LearningBefore our work in matchings and graphs, we began contributing to machine learning by combining discriminative (large margin) learning with generative (probabilistic) models. The machine learning community had two schools of thought: discriminative methods (such as large margin learning support vector classification) and generative methods (such as Bayesian networks, Bayesian learning (Pattern Recognition 00) and probability density estimation). Generative models summarize data and are more flexible since the practitioner can introduce various conditional independence assumptions, priors, hidden variables and myriad parametric assumptions. Meanwhile, discriminative models only learn from data to make accurate input to output predictions and offer less modeling flexibility, limiting the practitioner to explore kernel methods which can be less natural.The combination of generative and discriminative learning was explored in the book (Jebara 04) and provided several tools for combining these goals. These including variational approaches to maximum conditional likelihood estimation (NIPS 98, NIPS 00) as well as maximum entropy discrimination or MED (NIPS 99, UAI 00, ICML 04). These methods work directly with generative models yet estimate the models' parameters to reduce classification error and maximize the resulting classifier's margin. In fact, the MED approach subsumes support vector machines and also leads to important SVM extensions by using probabilistic machinery. This MED framework has led to the first convex multitask SVM approach which performs shared feature and kernel selection while estimating multiple SVM classifiers (ICML 04, JMLR 09). Similarly, nonstationary kernel selection and classification with hidden variables is also possible to derive using this framework (ICML 06). In current work, we are exploring variants of conic kernel selection by learning mixtures of transformations, a method that also subsumes SVM kernel learning (NIPS 07). Another approach to combining discriminative and generative learning is to use probability distributions to form kernels which are then used directly by standard large margin learning algorithms such as support vector machines. We proposed probability product kernels (ICML 03, COLT 03, JMLR 04) and hyperkernels (NIPS 06) which involve the integral of two probability functions over the sample space. This kernel is the affinity corresponding to the Hellinger divergence. This approach allows kernels to be built from exponential family models, mixtures, Bayesian networks and hidden Markov models. Since then, other researchers have extended this idea and developed kernels from probabilities by exploring other information divergences beyond the Hellinger divergence. While large margin estimation has led to consistent improvement in the classification accuracy of generative models and probabilistic kernels, our most recent work has been investigating even more aggressive discriminative criteria. This has led to a more powerful criterion for discrimination we call large relative margin. There, the margin formed by the classifier is maximized while also controlling the spread of the projections of the data onto the classification. This work has led to significant improvement over the performance of support vector machines without making any additional assumptions about the data. The extension of large margin approaches to the relative margin case is straightforward, efficient, has theoretical guarantees and empirically strong performance (AISTATS 07c, NIPS 08). We are currently investigating its applicability to large margin structured prediction problems, variants of boosting as well as the estimation of even more discriminative generative models. Application AreasIn addition to the above fundamental machine learning work, we are also dedicated to real-world applications of machine learning and its widespread impact on industry and other fields. In older work, we have built machine-learning inspired computer vision systems that achieved top-performing face recognition performance and obtained an honorable mention from the Pattern Recognition Society (Pattern Recognition 00, NIPS 98b). We have also worked on highly cited (300 citations) vision-based person tracking (CVPR 97), behavior recognition systems (ICVS 99) as well as mobile and wearable computing (ISWC 97, IUW 98). In early 2006, we helped found Sense Networks a startup that applies machine learning to location and mobile phone data. Other startups we are involved in include Agolo , Ninoh and Bookt.This page was last updated July 10, 2009. Old research statement. | |||||||||
|
|