 |
GPOTHELLO 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Hypothesis and Motivation How would we use genetic programming to have the computer learn to play Othello well? Neural Networks, Decision Trees, and Candidate Elimination gear more in the lines of "molding" a hypothesis(es) from a hypothesis space, but genetic algorithms take a different approach and require different thinking. We decided to have the computer learn from an already smart computer program, Edgar. The motivation here is you have to learn from someone smart to get smart, so learn from Edgar and evolve, mate, have children, do whatever it takes to beat Edgar. We believe that if our algorithm can beat Edgar or at least acquire a decent fitness from Edgar, our learned algorithm could most likely beat out the random players. So, Edgar will be one initial learning condition. Secondly, we'd like to create a scenario that would allow generating function trees faster (or dudes as George calls them) but produce positive results. Our hypothesis here is to use a smaller population but have more generations. We're trying to mimic the concept of evolution, by saying that the longer the populatoin exists (in terms of generations), the smarter the individual dudes will be. Along with that rational, we wanted to allow for more awkward growth, because just having generations and generations go by without having any random phenomenon happen would leave the population evolving perhaps in a pattern-like state, mating and conducting crossovers in the same fashion everytime. Rather than having this, why not throw a wrench in the system from time to time? In other words, we wanted to see how the populatoin would grow, and by allowing for mutations to occur about less than half the time, the population becomes much more interesting and diverse.
Dude A has potential to become better, and maybe by migrating him to the right population, he would produce lower fitness offspring (lower the better according to the GP program). We wanted to see what would happen if that occured 90% of the time. We believe that more migration will unlock "potential" for them (kind of like people migrating to the United States). To increase the number of our experimental runs, we decided to make the two above environments described (small pop, more gen, some mutation and demetic grouping, high migration) more situational, utilizing the three different selection types offered by the GPOthello.java program - Probability, Tournament, and Greedy Selection. This would give us a total of six distinct situational runs, enough to conduct a proper analysis on which had a better affect at achieving the smarts to beat Edgar. For those who don't know about the three selection types:
Approach and Modifications For some initial modifications, we decided to change the random number generator for the OthelloRandomPlayer algorithm. After inserting print statements, we saw that Random.nextDouble() did not do what it was supposed to, so we replaced it with the equivalent Java code, "Math.random();" to compensate. We changed the OthelloCache.java code so that the GPPlayer would be BLACK while Edgar or the RandomPlayer would play WHITE. This way we wouldn't have to constantly switch between the two colors for the GPPlayer. Our approach to satisfy our initial motive was to edit the GPOthello.ini file to modify the experiment for our specific environments: SMALL
POPULATION, MORE GENERATIONS, MUTATION (nicknamed Tribe):
For the above settings, there are 3 runs of each, each with a different selection type value - 0,1, or 2. They are the selection types I described above. Along with these settings, all 6 have these settings: number of games = 10; termination fitness = 1; good runs = 5.
We collected a few interesting results, but these results were not what we hoped for. This motivated us to produce better results, and we continued our experiment later with an altered motivation (will be discussed below). We tested our function trees against Edgar, playing one game with that program, and also tested it against random players, playing 50 games with those. We generated about 35 total trees. The greedy selection Immigrants and Tribe run consist of the bulk of the trees, because it ran the fastest at the Mudd NT Lab. The tournament selection Immigrant and Tribe runs were done on CUNIX, while the Probability Selection IM and TR runs were also done in the NT labs. Since CUNIX was mad slow, not too many trees came out of there. Analysis of our results show that the dudes that pitted badly against Edgar did relatively well against Random Players, which was half the effect we wanted to achieve. But we also wanted to beat Edgar as well. There is ONE dude that beat Edgar, but he barely beat him with a score of white/black - 31/33. He won by only two extra pieces. But as you see below (highlighted in blue), the program only won 7 out of 50 games against random players and this is consistently. What we learned here was that doing well against Edgar doesn't necessarily mean that we will do well against random players, although that might be perhaps intuitive, since we wouldn't be doing this if we could generate good othello players randomly. One reason we came up with for this discrepancy was that we overlearned to Edgar's strategy, leaving no room for any other type. By playing random players with a strategy meant to beat Edgar, we left our Edgar-creaming function tree unprepared to face randomness (these cases are pointed out below in the tables in YELLOW). Some other things we found interesting were that there wasn't much of a difference between choosing different selection types. Regardless of how the population chosen, things turned out very similar for probability, greedy, and tournament selection. With the Immigrants (Demetic grouped individuals) we saw that the trees were smaller than the ones with the smaller population. One thing positive was that we were able to see fitness improve as the generations evolved. Please check out the evolution of the only dude that beat Edgar.
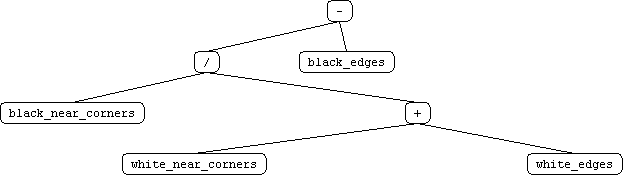
Post Experiment Success Story - Modified Hypothesis Here is probably where we made an important move towards trying to beat Edgar and at the same time beat Random Players. Thinking back on overlearning for Edgar, the tree right above doesn't really learn Edgar too well, since the score in the end is about even (31/33). This tree is still the smartest one out of the bunch, and we began to think of other possible ways to improve this particular tree. Our new hypothesis was since this tree already learned so much, why couldn't it possibly be a structure for something that CAN work for both random players and Edgar. Here, we decided to keep the tree structure constant, and randomly choose either 1) the leaves/primitives or 2) randomly choose the operators. Our rational for this is that the tree has already provided enough information to do damage to Edgar, but it perhaps needs a little fine tuning. The hypothesis space has already been trimmed down, and now we just need to refine it, and that's where either the leaves are altered, or the internal nodes are altered. Here is the tree above in prefix format: - / black_near_corners + white_near_corners white_edges black_edges. In other words: operator operator primitive operative primitive primitive primitive (3 ops, 4 prims) First we decided to fix the operators to their preset value, randomizing the primitives. Then we tried the opposite. For the former and latter, we ran a perlscript that George wrote that would generate semi-random function trees that were then put to the test on Edgar. WE HAD GREAT RESULTS, and we came up with one final tree that BEAT EDGAR and BEAT RANDOM PLAYERS. I welcome you to take a look at our algorithm vs. edgar and our algorithm vs. a random player. There were some problems with the applet aspect of it, and for some reason it didn't load in Netscape. The results are below: RP = Random Primitives, RO = Random Operators
I welcome you to try these trees. The best two trees above in blue are the ones that do highly well against Edgar and highly well against random players. Loosing to one tree above by a score of 23/41 pretty much guarantees a win over Edgar anyday, and on average and consistently, this tree could win about 41 times out of 50! We ran it a few more times to make sure, but that was the final verdict. I end this experiment with these set of very good modifications to the original tree that beat Edgar. You are welcome to look at the data that we have collected.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
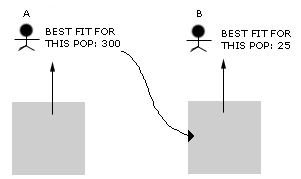A
third approach we decided to adopt is the use of demetic grouping, messing
around with populations separated from one another. With only one large
population, dudes that are less fit will mostly likely not have a chance
to mate, and they get lost in evolution. We wanted to save those dudes
from extinction, by separating the population into five groups, each
group having their own relatively fit dude. One of the dudes might not
be fit for its current generation, but it might have the potential to
become something better after crossover. For example, say we have two
populations, and two relatively fit individuals (see left).