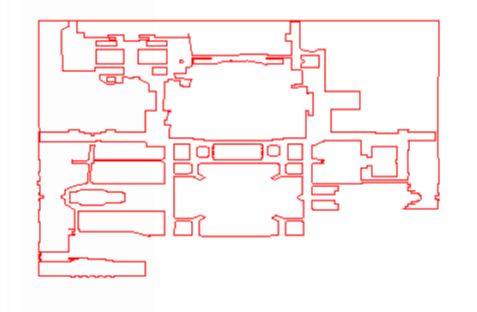
The two-dimensional map of the robot's test area,
the northern half of Columbia's Morningside Campus.
In this page, I give a brief overview of my work on the development of an efficient and robust algorithm for computing safe paths for a mobile robot. I have specifically designed the algorithm for use in the Autonomous Vehicle for Exploration and Navigation in Urban Environments (AVENUE) project. The environment currently being investigated is the Morningside Heights campus of Columbia University, but will eventually be expanded to other urban areas. In the general problem, one is given a two-dimensional map of the complicated region in which a robot will be operating. Such a map includes a variety of polygonal obstacles that are to be avoided. To determine paths along which the robot can safely move through this environment, I use an approach based on the generalized Voronoi diagram for a planar region with specified obstacles. Once this diagram has been constructed, I can search it to find robot paths that pass, with maximal clearance, around the obstacles.

The two-dimensional region in which the robot moves will contain buildings and other types of barriers, each of which can be represented by a convex or concave polygonal obstacle. To find the generalized Voronoi diagram for this collection of polygons, one can either compute the diagram exactly or use an approximation based on the simpler problem of computing the Voronoi diagram for a set of discrete points. In my work, I use the latter method. First, I approximate the boundaries of the polygonal obstacles with the large number of points that result from subdividing each side of the original polygon into small segments. Second, I compute the Voronoi diagram for this collection of approximating points. Once this complicated Voronoi diagram is constructed, I then eliminate those Voronoi edges which have one or both endpoints lying inside any of the obstacles. The remaining Voronoi edges form a good approximation of the generalized Voronoi diagram for the original obstacles in the map. In this Voronoi diagram, I locate the robot's starting and stopping points and then compute the Voronoi vertices which are closest to these two points. I then use straight lines to connect the robot's starting and stopping points to these closest vertices. Special consideration is given to those situations in which one or both of the connecting straight lines pass through an obstacle. Once I have determined the starting and stopping vertices on the Voronoi diagram; I can implement a standard search, such as Dijkstra's Algorithm, to find a "best" path which is a subset of the Voronoi diagram and which connects the starting and stopping vertices. This path can then be expanded to a path between the robot's original starting and stopping points. The method generates a route that for the most part remains equidistant between the obstacles closest to the robot and gives the robot a relatively safe path along which to travel.
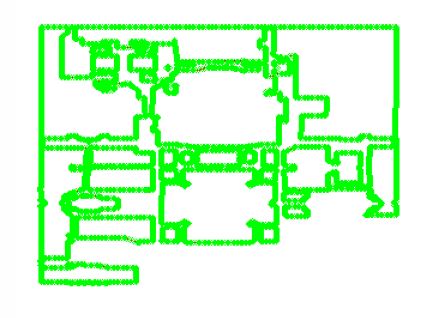 The points that approximate the polygonal obstacles. |
 The Voronoi diagram for all of the points generated in the approximation. |
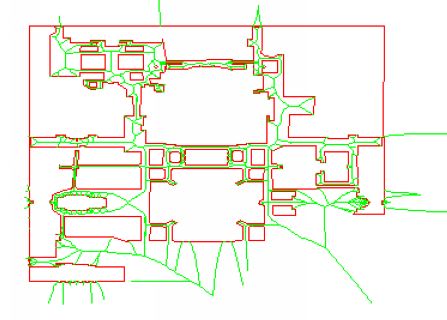 The Voronoi diagram after the elimination step. |
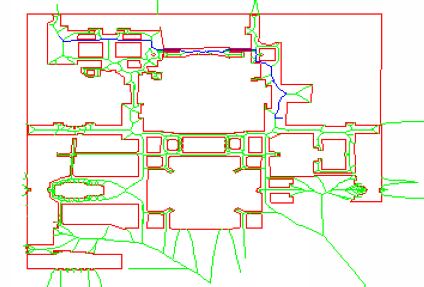 A sample path chosen along the Voronoi diagram by the search algorithm. |
The following is a Java applet that demonstrates the path planning algorithm in action and gives an example of the user interface. In red is the campus map, and in green is the generalized Voronoi diagram computed for this map (which the applet precomputed). To compute a path, first click on a starting point and then click on a stopping point. Finally click "Compute Path". Despite its small appearance, this map is actually composed of thousands of points. Therefore it can take up to 30 seconds to compute a path, depending on the speed of your computer.
Click here for the applet.