Motivation: There have been many works demonstarting strong feasibility results for the secure computation of any function in time polynomial in the size of its Boolean or arithmetic circuit. However, these generic approaches typically lead to inefficient implementations since the circuit representation of a functionality may be very large. Thus, an important problem in MPC is designing highly efficient protocols for smaller, yet large enough to be interesting, sets of functionalities (election problems is a narrow example, while linear algebraic problems is a more generic example).

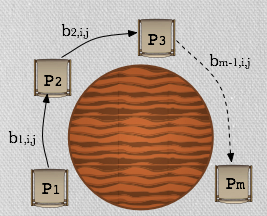
We consider the problem of secure multiparty computation of the class of functions that can be represented by polynomial-sized multivariate polynomials. The multivariate polynomial is defined over the inputs of the participating parties so that each party contributes its inputs as values for some subset of the variables in the polynomial representation. There is a designated party receiving output that learns only the output of the polynomial evaluation while all other parties receive no output. (We note that our protocol can be generalized to allow any subset of the parties to receive output.) We are interested in these functions since a large collection of problems are naturally and efficiently represented as multivariate polynomials over a field or a ring: problems from linear algebra, statistics, logic as well as operations on sets represented as polynomials.

Results: Our first result is a construction for two party set intersection protocol that provides security against malicious adversaries in the standard Real/Ideal model. It improved the efficiency of exisiting solutions in the same adversarial model.

We extended the techniques from our set intersection result to build a protocol that allows multiple parties to compute the above functionalities, assuring security against a dishonest majority and robustness (detection misbehavior). Our protocol is fully black-box assuming any threshold homomorphic encryption with a natural property that we specify later, (instantiated by Paillier scheme, say). It utilizes what is known in the past as a "round table" structure where parties are nodes in a ring network (which means that frequently a party only communicates with the consecutive parties around the table). This structure has two benefits: first, it allows each party to be offline for the majority of the execution of the protocol and to be involved only when it needs to contribute its inputs at its turn. Second, it allows a division of the communication complexity into two types: "round table" communication complexity including messages exchanged between two consecutive parties, and broadcast communication complexity including messages sent simultaneously to all parties. We give simulation-based proofs of security in the Ideal/Real (standard) Model. Our work improves the communication complexity of the protocol presented [FM'10] (the only previous work that we are aware off that focuses on multivariate polynomial evaluation). [FM'10] focuses on polynomials of degree 3 and leaves as an open question the construction of specialized protocols for polynomials of degree higher than 3 that do not rely on generic MPC techniques, and our work gives such a construction.