Reasoning in Multi-Context Systems
Overview
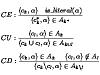
The reasoning process is broken into local reasoning fragments each of which is associated with a context. A context is thought of as a logical theory presented as an axiomatic formal system consisting of a language, a set of axioms and a set of inference rules. A multi-context system is defined as a pair of a set of contexts and a set of bridge rules -- inference rules switching the reasoning process from one context to another.
Two separate sets of context inference rules are discussed and their equivalence is proved. The most important result is that the consistency of one context does not depend on the consistency of any other context.
A set of operators for building a variety of compound contexts on the basis of the initial ones is defined and demonstrated through examples. A sample Prolog meta-interpreter is presented as an illustration of some of the advantages and some of the problems from the implementation point of view. Some ideas for further extensions of this model are also outlined.
Publications
-
Reasoning in Multi-Context Systems
MS Thesis, Faculty of Mathematics and Informatics, Sofia University, Sofia, Bulgaria, May 1996.
(Advisor: Prof. Christo Dichev)

