Reference: An Algorithm for Planning Collision-Free Paths Among Polyhedral Obstacles by Lozano-Perez and Wesley.

(70 points) Part I: Write a progam to do 2-D collision-free motion planning. Your program will take as input a file which contains sets of ordered vertices of convex polygons which represents a set of obstacles in your world, along with a bounding box around the entire environment. You will grow these obstacles by the size of the Create robot (we will give you its convex polygonal dimensions) using the reflection algorithm and the convex hull algorithm discussed in class. Then, given an arbitrary start and end point in this environment, create a Visibility graph on these grown obstacles, and search it using Dijkstra's algorithm to find a safe, collision free path. Your program should graphically draw the following (see figure 3b below). You may use the programming language of your choice for this assignment.

• The start point
• The goal point
• The obstacle set
• The grown obstacle set
• The Visibility Graph
• The safe path

Figure 1: Sample output for homework 4

1. Original Obstacles (plus wall boundary) & Start and End Points
2. Grown Obstacles
3. Visibility Graph
4. Shortest Path

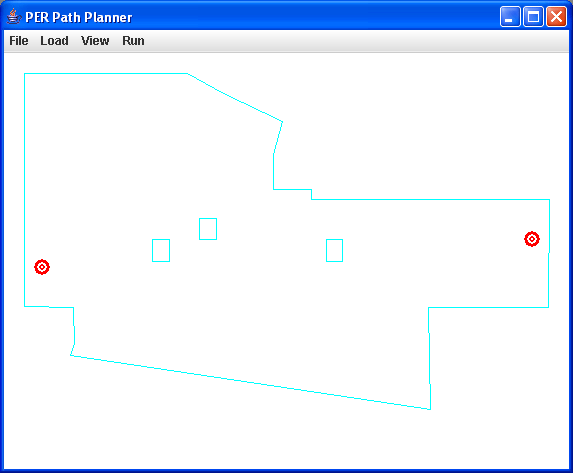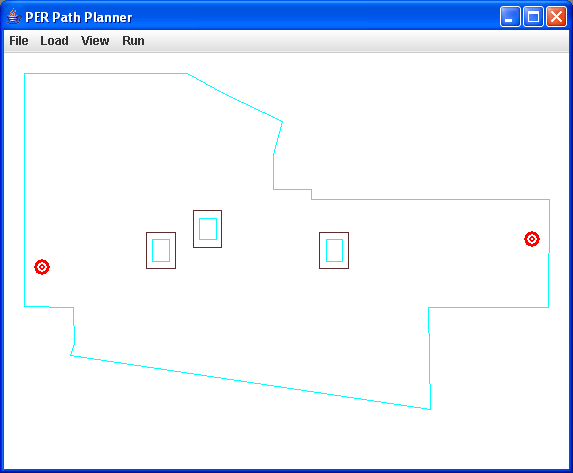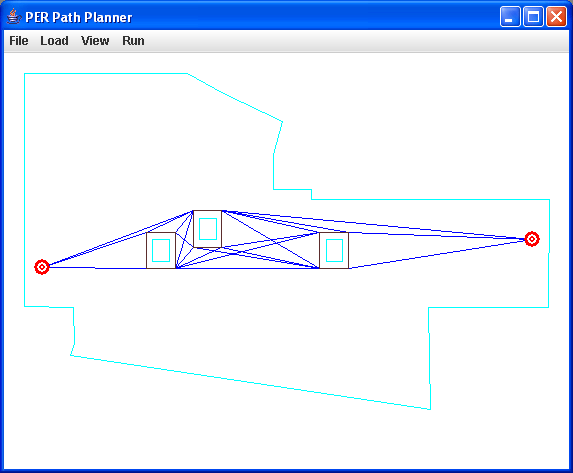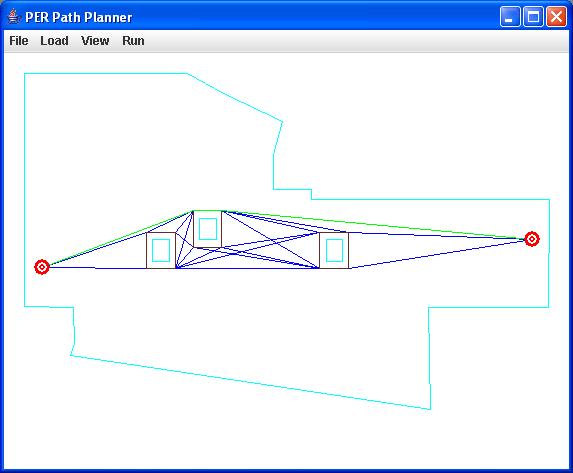
Note 1: your program should create a safe path (if one exists) for any file of obstacles we give you, not just the test case.

Note 2: You do now have to grow the walls that enclose the working environment, you may assume that these are already grown obstacles.

Text file containing the description of the obstacles. Format is as follows

• first integer gives you the number of obstacles
• for each obstacle:
• first integer gives you the number of vertices
• the vertices follow as X Y pairs, one per line, each with two coordinates
• you should close the obstacle by linking the last vertex to the first
• the first obstacle in the file actually specifies the wall that encloses the working environment.

• first line (X Y coordinates) determines the start point
• second line (X Y coordinates) determines the goal point

Here is a picture of the start, goal and obstacles environment you will use for Part II below. Please note that for both sets of data, the X-Y axes are aligned with Z pointing up.

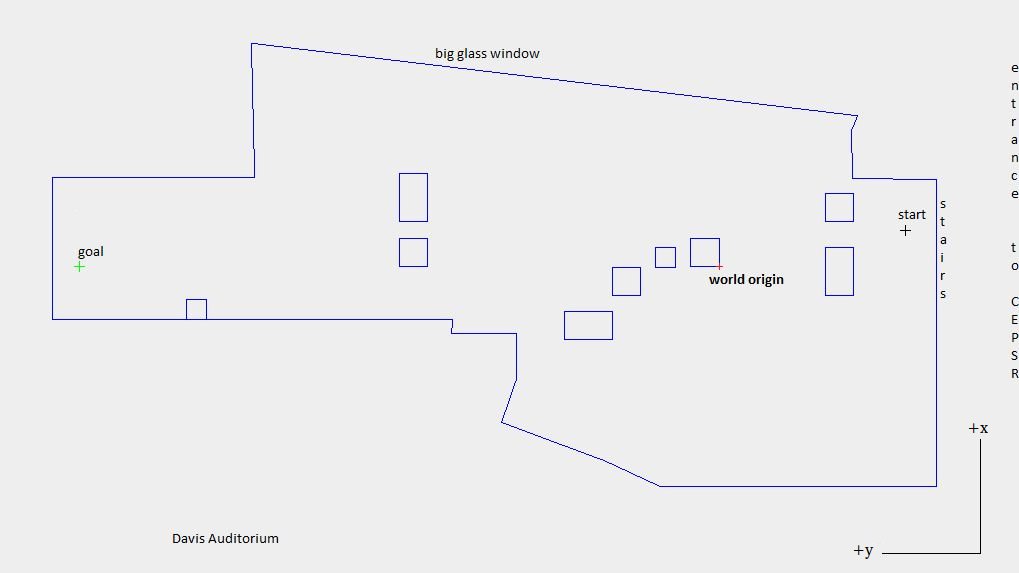
(30 points) Part II: ROBORACE 2015 Use your solution to generate path commands to have your Create robot follow the solution you computed above. We will set up a physical obstacle course and see which group's solution is the best: fastest and collision free, with prizes awarded to the winning groups. We will run the race during class time on Nov. 19 outside Davis Auditorium.

• Extra Credit: (10 points) Create's are known to have poor odometry. Extend your path planner to take into account "bumping" into obstacles due to poor odometry. Your planner should react by trying to figure out which obstacle it hit and replanning its path based upon this new info.

• Extra Credit: (10 points) You may also use your robot mounted camera to visually "steer" away from obstacles your robot may encounter on its computed path.