
An important aspect of any rapid prototyping system is the speed with which it can acquire a complete model from a set of incomplete views of the model acquired from a sensor. As with segmentation all but the simplest objects will require that each view be merged with the others, often a difficult and time-consuming preocess. There are a variety of methods used to merge multiple views of an object together, including methods based on Constructive Solid Geometry, volumetric approaches, and [add one more here]. These are all highly dependent on the object representation being used. The desiderata for a representation are that it be effective at modeling the segmented data of each view and be able to quickly merge the different views into a single, accurate representation of the data. Such a representation is the Binary Space Partitioning Tree, or BSPT.
A BSPT is a method by which n dimensional space is partitioned by n-1 dimensional entities called hyperplanes. For example, 2D space would be partitioned by 1D entities, i.e. lines, and 3D space would be partitioned by 2D entities, i.e. planes. Once a space has been partitioned by a hyperplane, it is represented by two n dimensional spaces, one on each side of the partitioning hyperplane.
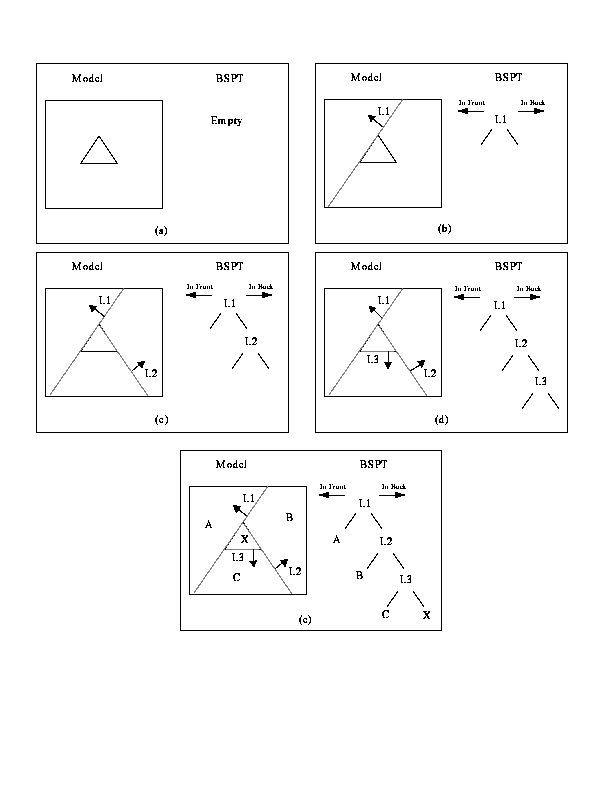
An effective way to understand the use of a BSPT is to follow a simple example of their construction, which can be done by a 2D example. Suppose one wishes to generate the BSPT representation of a triangle (See the figure below), beginning with an empty BSPT. To process starts by choosing a hyperplane to partition the space, say L1. If a normal is associated with L1, this partitions the space into two half-spaces, space in front of L1 and space behind it. The two half-spaces are then recursively partitioned until the homogenaity constraint is met. Note that it is only necessary to partition a half-space if it is not homogeneous. In this case, the space behind L1 is not homogeneous, so we will contine to partition it. The remaining figures show a continuation of this process, until the model is completely partitioned. By labeling the regions paritioned by the complete tree, it can be seen that each region is described by a leaf in the tree, while each internal node describes both an edge of the model and a hyperplane.

An analogous procedure may be followed to build a BSPT of a 3D space, using planes as the partitioning hyperplanes instead of lines as in the 2D example.
The BSPT has unique advantages as an intermediate representation for the different views. Its tree structure allows very efficient algorithms to be developed, it is compact, and it is numerically robust. The BSPT representation has proven its utility in 3D modeling , in graphics, and in image processing as a tool for representation and compression. Of primary importance for this work is that there exist very fast and robust algorithms for merging models represented as BSPTs. If, after segmentation of each laser image, we build a BSPT representing each image, we may then use boolean operations to get the intersection of these images. This intersection will be those parts in the model that all the views, together, can determine.