Specularities in Stereo and Motion |
 |
|
When an observer moves in three-dimensional space, real scene features, such as surface markings, remain stationary with respect to the surfaces they belong to. In contrast, a virtual feature, which is the specular reflection of a real feature, travels on the surface. Since algorithms for stereo and structure from motion do not distinguish between real and virtual features, they end up producing incorrect depth information in the case of specular objects. Sometimes the computed structure can be significantly different from the actual structure of the object. In this project, we are investigating techniques that enable stereo and structure from motion to detect and handle specular reflections.
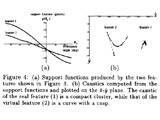
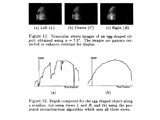
The first part of the project focuses on the recovery of a specular surface using a moving camera with known motion. Based on the notion of caustics, we have developed a novel feature classification algorithm that can distinguish real and virtual features from their image trajectories due to camera motion. Next, using support functions of curves, a closed-form relation is derived between the image trajectory of a virtual feature and the geometry of the specular surface it travels on. It is shown that when the camera motion and the surface profile are coplanar, the profile is uniquely recovered by tracking just two unknown virtual features. These results have also been extended to the case of arbitrary 3D surface profiles that are traveled by virtual features when camera motion is not confined to a plane. In the second part of the project, we have studied the the problem of accurate depth estimation using stereo in the presence of specular reflections. Since specular reflection is viewpoint dependent, it can cause large intensity differences at corresponding scene points in a stereo image pair. This results in significant errors in the computed scene structure. We have analyzed the physics of specular reflection and the geometry of stereopsis and arrived at a relationship between stereo vergence, surface roughness and the likelihood of a correct match. Given a lower bound on surface roughness, an optimal binocular stereo configuration can be determined which maximizes precision in depth estimation despite specular reflection. However, surface roughness is difficult to estimate in unstructured environments. Therefore, trinocular configurations that are independent of surface roughness are determined such that at each scene point that is visible to all three cameras, at least one stereo pair can produce correct depth. We have developed a simple algorithm to reconstruct depth from the multiple stereo pairs. Finally, we have developed ordinal measures (which are based on rank-permutations of intensity values) for solving correspondence and tracking problems in stereo and motion. We have shown that ordinal measures are more robust to non-ideal imaging conditions than the more commonly used correlation and the sum of squared difference measures. |
Publicationsprint_paperentry_byid: more than 2 or no entry matches. |
Pictures |
Related ProjectsShape from Brightness |